Contents

Pre Lab 5

Here are some help for pre lab 5

Part 1

  • In terms of the potential, the component of the electric field in the s-direction is \(E_{s} = -\frac{\Delta{V}}{\Delta{s}}\) (\(\Delta{V}\) is the potential difference between the two points, \(\Delta{s}\) is the small distance between to points i and f. In the limit \(\Delta{s}\)→0:

\[E_{s} = -\frac{dV}{ds}\]

  • The formula is derived as such:

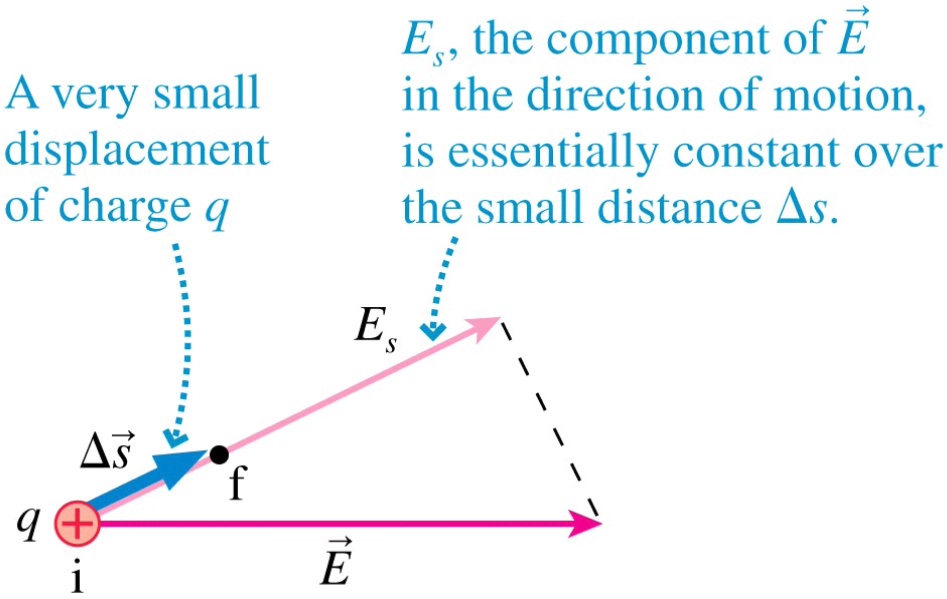
../../_images/concept_lab5.jpg

Fig. 21 Relationship between electric potential and eletric field

  • Question: Why is this important? Answer: The electric field is the negative of the slope of potential vs distance graph!

  • Let’s have an example (bottom-right):

import matplotlib.pyplot as plt
import matplotlib
import numpy as np

matplotlib.pyplot.ion()

# Initialize some constant
k = 9 * pow(10,9)
def find_V(x_array, q=pow(10,-9)): # Default q=1nC
    with np.errstate(divide='ignore', invalid='ignore'):
        return (k * q)/x_array

def find_E(x_array, q=pow(10,-9)): # Default q=1nC
    # Basically -(-(k*q)/x^2) but altogether gives +
    with np.errstate(divide='ignore', invalid='ignore'):
      return (k * q)/pow(x_array,2)

# Sample size
n = 201
x_lim=20
# Generate a random dataset
sample_x = np.linspace(-x_lim,x_lim,n)
#sample_x = np.linspace(-10,10,101)
# print(sample) Debugging

# Customize figures and plots
fig_kw = {'color':'r','linewidth':4.0}
fig, ax = plt.subplots(nrows=1,ncols=2) # Create a figure with 
fig.tight_layout()
fig.figsize=(20,20) # 20x20 inches

def customize(ax):
    ax.spines['right'].set_visible(False)
    ax.spines['top'].set_visible(False)
    ax.axvline(x=0, color='red',linestyle=":")
    return ax


# Set up for V graph
ax[0].plot(sample_x,find_V(sample_x))
ax[0].set(title=r"$V_{x}\ vs\ x$", 
          ylabel="Electric Potential (V)",
          xlabel="x(m)", 
          label=r"$V(x)= \frac{k*q}{x}$")
customize(ax[0])

# Set up for E graph
ax[1].plot(sample_x, find_E(sample_x))
ax[1].set(title=r"$E_{x}\ vs\ x$", 
          ylabel="Electric Field (V/m)",
          xlabel="x(m)",
          label=r"$E(x)= -\frac{k*q}{x^2}$")
customize(ax[1])

# fig.show()

<matplotlib.axes._subplots.AxesSubplot at 0x7fa4c833a250>
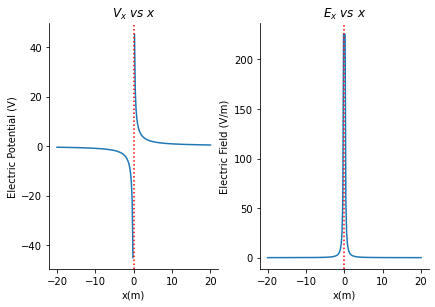
../../_images/prelab5_2_1.png

Caution

Use only the portion where x >= 0. Distance cannot be negative right?

Part 2

  • Our question is:

Explain why a conductor in electrostatic equilibrium should have no electric field parallel to its surface, nor within its bulk. (Hint: think about the forces on a free to move cha,rged particle

  • Few things to consider about conductors:

    • Electrostatic means no net movement of charges.

    • Charges in a conductor are free to move (does not mean they are moving!).

  • Few basic concepts about electric fields:

    • Electric field is the distorted space (by a charged source object) that exerts electric force on any charge surrounding charged objects.

    • If there is a force that disturbs equilibrium, acceleration is present, meaning things are moving.

Tip

Use contradiction to prove this!

  • Now, the question should be clear. Answering this will also give you an idea why the electric field is only available at the surface and perpendicular to the surface.

  • A picture for you:

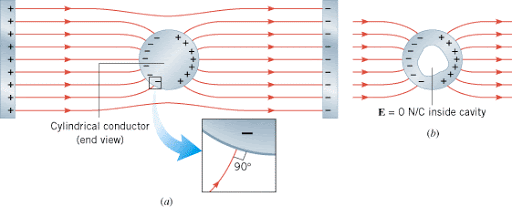
../../_images/conductor.gif

Fig. 22 Electric field outside a conductor

See also

A conductor is an equipotential surface. That means \(\Delta{V} = 0\) everywhere inside it.

Part 3

  • Our question is:

When a steady current I is flowing through a conductor with a non-negligible resistance R, it will be possible to maintain a potential difference \(\Delta{V} = I*R\) between parts of the conductor along the direction of the current. Explain why in this situation there should be an electric fieid in the direction of the current but not in the direction perpendicular to the current.

  • Now, a few things to consider:

    • The above concepts about electric fields.

    • With a current inside a conductor, the charges are moving, driven by an electric field in the same direction.

    • This field is originated from the potential difference between upstream and downstream of the source (i.e. battery).

  • A picture for you to understand what I am saying:

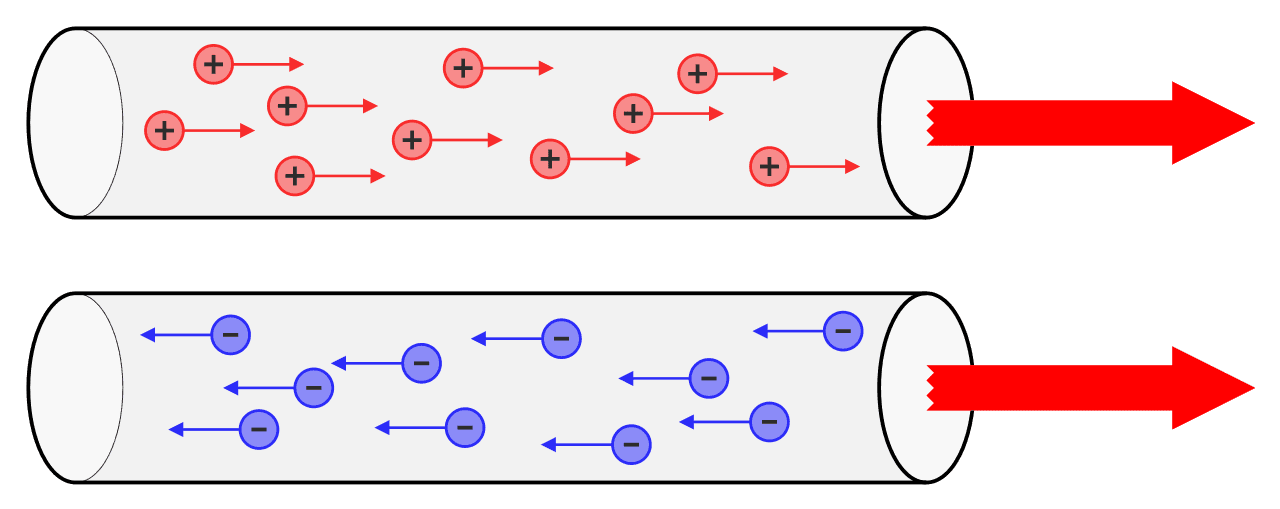
../../_images/current_lab5.png

Fig. 23 The behind-the-scence of electric current

  • Now, those help answer the first part of the question. The seccond needs some imagination:

    • Think of conductor as a metal wire.

    • Now, an electric field perpendicular to the current will drive the current a way such that it is closer to the surface. Right?

    • Now, let’s answer these:

      • Can the charge escape the conductor to the environment?

      • If not, how does it behave?

Tip

Is there a disturbance to the flow? Anything stuck?

Lab 5 Lab 6